Ball bearings perform their functions by rotating, but they also generate vibration.
The vibration whose frequency changes depending on the rotation speed is called the "vibration by forced rotation".
Calculation of vibration by forced rotation
The vibration is generated in axial, radial, and rotating directions. Depending on the product in which rolling ball bearings are used, the vibration has a significant impact on performance.
This vibration sometimes causes components around the axis to resonate as vibration energy is emitted.
It is necessary to understand the application characteristics well in order to select a suitable bearing, and its specification.
Formula for inner ring rotation
Dw : Ball diameter (mm)
Dpw : Pitch circle diameter (mm)
α0 : Nominal contact angle (°)
Z : Number of balls
n : Integer number
fr : Inner ring rotation speed (Hz)
Fr : Outer ring rotation speed (Hz)
To simplify, cos α0 = 1 could be used.
Formula for outer ring rotation
The calculations below are examples.
Example.1 :
When the inner ring of an R-1560X2ZZ bearing is rotated at 1,800 min-1, vibration caused by ball revolution is calculated as follows:
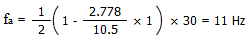
As the difference in each ball gets bigger, vibration in the rotating direction also increases (Figure 15-1, 15-2).
Example 2 :
The amplitude of vibration at the vibration position calculated above for this R-1560X2ZZ bearing increases when the inner and outer ring raceways deform to hexagonal, heptagonal, and octagonal shapes (Figure 15-3, 15-4, 15-5, 15-6).
Normal rotational vibration
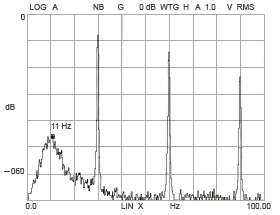
Figure 15-1
Rotational vibration when the difference between balls is large
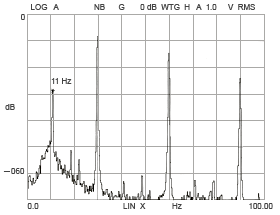
Figure 15-2
Outer ring raceway deformation
(Shape)
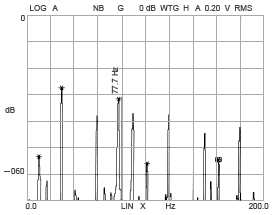
Figure 15-3
Inner ring raceway deformation
(hexagonal shape)
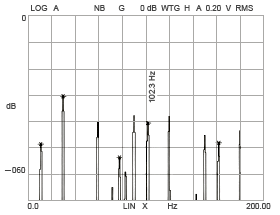
Figure 15-4
Inner ring raceway deformation
(heptagonal shape)
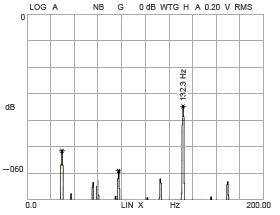
Figure 15-5
Inner ring raceway deformation
(octagonal shape)
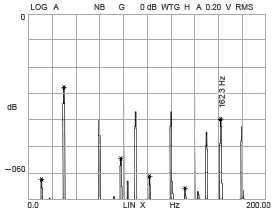
Figure 15-6