Metal/Metal spherical bearing
Metal/Metal types are mostly applied under static load, which does not require rotating movement, and therefore, the load capacity shall be calculated under the static load. However a spherical bearings with Al-Bz race material, almost no seizure occurs under oscillation or limited lubrication supply. Also, Be-Cu ball and stainless steel race can prevent seizure under heavy load and can provide high dynamic load carrying capacity. From these facts, capacity under slow fluctuation velocity shall be also calculated. When static load capacity is more crucial than oscillation load capacity, steel ball and steel race is the most suitable combination. It is not able to maintain sufficient lubrication in order to bring out most of Metal/Metal type characteristics.
Definition of Load
Directions of load application are indicated in Figure 5.
Figure 5: Directions of load applications
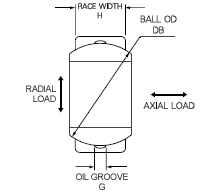
Static Limit Load
Static limit load is the load, which can be applied without disturbing the performance of Spherical Bearings. Minebea specifies that the permanent deformation shall no exceed the value in Table 5 when this load is applied statically.
Table 5 : Permanent deformation under static load
| | Maximum value |
|---|---|
| Radial Static Limit load | 0.076mm |
| Axial Static Limit load | 0.102mm |
Static Ultimate Load
This is the load, which can be applied to Spherical Bearings without distracting it. Static ultimate load is 1.5 times the static limit load.
Oscillating Load
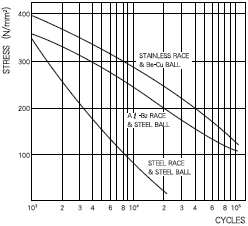
This load can bear the oscillation test condition of : oscillation angle ±10°, frequency of 10cpm, and alternating load. The radial play including abrasion does not exceed 0.102mm after 20,000 cycles.
Figure 6 shows the relation of surface pressure and life cycle of bearing from this test.
Figure 6: Relationship between Stress and Life of Metal/Metal Spherical Bearings.
Calculation of load capacity
Load capacity (W) could be calculated as: race projected areas (SR or SA) multiplied by the race allowable stress (σ)
W = (SR or SA) × σ
Radial projected area (SR)
The shaded area in Figure 7 is radial projected area.
It can be calculated by the formula: SR = H × DB.
It shall be noted that where there is an oil groove, it should be subtracted from this formula.
Axial projected area (SA)
The shaded area in Figure 8 is axial projected area.
It can be calculated by the formula: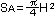 
-
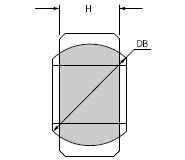
Figure 7:
Radial Projected Area
-
Figure 8:
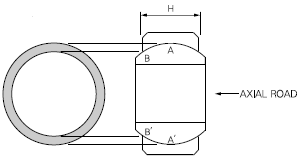
Axial Projected Area
Allowable stress (σ)
The Allowable stress may vary depending on materials and heat treatment condition. Minebea set the allowable stress as indicated in Table 6 and 7, based on various examinations.
Table 6 : Allowable Static Race Stress
| | 4130or Stainless Race (30-35HRC) | Al-Bz Race |
|---|---|---|
| Radial Static Limit Load | 620N/mm2 { 63.3kgf/mm2 } | 379N/mm2 { 38.7kgf/mm2 } |
| Axial Static Limit Load | 551N/mm2 { 56.2kgf/mm2 } | 275N/mm2 { 28.1kgf/mm2 } |
Table 7 : Allowable Dynamic Race Stress
| | Dynamic Load |
|---|---|
| Al-Bz Race Steel Ball | 193N/mm2{ 19.7kgf/mm2 } |
| Stainless Steel Race Be-Cu Ball | 241N/mm2{ 24.6kgf/mm2 } |